『シンメトリーとモンスター』 マーク・ロナン (岩波書店)
群論の研究者が書いた一般向けの本だが、内容はかなり高度である。
日本版の副題は「数学の美を求めて」だが、原著では「もっとも偉大な数学の探求の一つ」となっていて、著者自身が参加した「アトラス(地図帳)計画」をさす。
群論を開拓したガロアは群を部分群に分解していくと、それ以上分解できない単純群と呼ばれる特別な群に行き着くことを発見した(単純群とは整数論における素数のようなものといえるかもしれない)。「アトラス計画」とは、この単純群をすべて分類しつくそうという壮大な計画で、1960年代にはじまった。当初は終わりがあるのかどうかもわからず、すくなくとも20世紀中には終わらないだろうと言われていたが、1980年頃には終わってしまい、1985年から電話帳のような『アトラス』の刊行がはじまった。
めでたしめでたしと言いたいところだが、探求の過程で「モンスター群」と呼ばれる巨大な群が見つかり(最小のものでも19万6883次元空間にある!)、しかもその次元数が整数論の鍵のなる数と1違いということがわかった。モンスター群の巨大な次元数と整数論の鍵となる数の一致はそれ以外にも続々と見つかり、まったく違う分野だと考えられてきた群論と整数論の間に秘められた関係があるのではないかという新しい課題が姿をあらわしてきた。これをムーンシャイン問題という(ムーンシャインとはアイルランドの妖精が月明かりを浴びて踊る情景を意味すると同時に、禁酒法時代の密造酒の意味もあるよし)。
本書は群論の歴史をふりかえりながら、「アトラス計画」の完成とモンスター群の出現(モンスター群は素粒子論や超弦理論と関係があることがわかってきた)、ムーンシャイン問題という最新の話題をカバーしている。
群論は方程式の解法を探す過程で生まれたが、本書は群論の基礎にある対称性を重視し、プラトン立体からはじめている(現代の群論は幾何学との関係が深いそうであるが、本書も幾何学を前面に出している)。
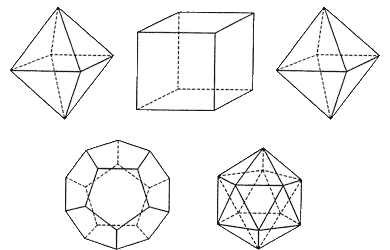
正三角形4面からなる正四面体、正方形6面からなる正六面体(立方体)、ピラミッドを二つ底面で貼りあわせたような正八面体、五角形12面からなる正一二面体、正三角形20面からなる正二十面体はプラトンの学園にいたテアイテトスが発見したとされているのでプラトン立体というが、きわめて対称性の高い図形であることは一目でわかるだろう。
対称性が高いといっても、それは印象にとどまり、数学的に語る方法がなかった。
対称性を数学の問題として厳密に語れるようになったのはガロアが群論の基礎を築いてからである。本書にもガロアと5次方程式の話は出てくるが、全17章のうちの1章にすぎない。
本書のヒーローはガロアよりもむしろソフス・リーである。
リーはアーベルと同じくノルウェイの牧師の息子として生まれたが、夭折したアーベルと違い頑健な巨体と体力に恵まれ、郷里では「良い子にしなさい。さもないと、ソフス・リーが来て、あなたを連れていってしまうわよ」と言われていたそうである。普仏戦争の時にはちょうどパリに遊学していたが、戦乱の中を徒歩でイタリアまで行こうとし、スパイ容疑で一ヶ月間監獄暮らしをする破目になったという武勇伝まで残っている。
リーは曲線や曲面のような連続に変化するものを有限の構造に落としこむ方法を開発し、後にリー群とかリー代数と呼ばれる新分野を切り拓くが、ガロア理論のようになかなか理解されなかった。しかしリーは57歳まで生きたので、多くの論文を書き弟子を育てることができた。
連続を有限の構造に落としこむといわれても雲をつかむような話であるが、著者のロナンは例としてコンピュータの2進法をあげ、音声や画像を周期2の有限代数系に落としこんでいるとしている。
よくわからないのであるが、単純群探しにはリー群が大活躍するそうで、後半は「アトラス計画」の話になっていく。2129万6876次元空間とか、8億4260万9326次元空間、185億3875万76次元空間等々、途方もない数字が次から次へと出てきて、頭の中が真っ白になる。
最後の方で超ひも理論の26次元空間や10次元空間が出てくると、なぜかほっとしてしまった(どちらもわからないのであるが)。
とうてい理解できなかったが、群論の最先端をちょっとだけのぞかせてもらい、こういう世界もあるのだなあと嘆息した。
